[자료구조] B+트리의 개념과 B-트리와 비교

B-트리

구조적 특성

• 내부 노드는 키 값과 데이터(디스크 주소)를 함께 저장하며, 키 값에 해당하는 데이터를 직접 반환할 수 있다.
• 리프 노드 역시 키 값과 데이터(디스크 주소)를 저장한다.
• 내부 노드와 리프 노드는 서로 독립적으로 키 값을 저장하며,
  1. 내부 노드의 키 값은 리프 노드에 존재하지 않는다.
  2. 리프 노드의 키 값 또한 내부 노드에 존재하지 않는다.
• 리프 노드는 별도의 링크 없이 개별적으로 존재한다.

 

B-트리의 순차 검색의 문제점 (랜덤 검색 발생)

B-트리에서는 연속적인 키를 순차적으로 검색할 때, 각 키의 위치가 내부 노드와 리프 노드에 나뉘어 있기 때문에 다음과 같은 문제점이 발생할 수 있다.

• 내부 노드에서 하나의 키를 찾은 후, 다음 키가 리프 노드에 있을 경우 디스크 I/O가 추가적으로 발생한다.
• 리프 노드 간에 직접 연결이 없으므로, 다음 키를 찾기 위해 부모 노드를 통해 경로를 다시 랜덤 탐색(Random Access)해야 하는 비효율성이 발생할 수 있다 

예를 들어, 키 10을 찾은 후 키 20을 찾고 싶다고 가정하자.

• 탐색 과정:
  1. 10을 찾으면 리프 노드 [5, 10]에서 찾을 수 있습니다.
  2. 20을 찾으려면 상위 노드 [15]로 올라가서 15보다 크므로 오른쪽 서브트리로 이동합니다.
  3. 오른쪽 자식 노드 [20, 25]에서 20을 찾을 수 있습니다.

특징)

• 부모 노드를 통해 오른쪽 자식 노드로 이동하여 탐색이 이루어짐.
• 부모-자식 간의 관계를 통해 탐색 경로를 따라갑니다.
• *트리의 구조를 따라 불규칙적인 디스크 블록 접근 발생

이러한 이유로, B-트리는 순차 검색이 비효율적이며 랜덤 검색처럼 작동할 수 있습니다.

 

랜덤 탐색(Random Access)의 영향

1. 디스크 I/O 증가
2. 연속적인 키 검색 시에도 여러 블록을 불규칙적으로 접근해야 하므로, 디스크 성능 저하
3. 캐시 효율성 감소
4. 순차적인 접근이 아니라 여러 노드로 이동하므로, 메모리 캐시 효율이 떨어질 수 있음
5. 범위 검색의 비효율성
6. 특정 범위의 데이터를 검색하려면 여러 번 부모 노드를 경유해야 하므로 범위 쿼리에 비효율적

 

트리의 높이

내부 노드에 데이터를 저장하므로 B+트리에 비해 키 개수가 제한되어 트리의 높이가 상대적으로 높아질 수 있다.

B-트리가 B+트리보다 트리 높이가 높은 이유

1. 내부 노드 저장 방식의 차이
   • B-트리는 내부 노드가 키와 데이터(디스크 주소)를 함께 저장하므로, 하나의 노드에 저장할 수 있는 키 개수가 제한됨
   • 반면, B+트리는 내부 노드가 키 값만 저장하므로 동일한 크기의 노드에서 더 많은 키를 저장할 수 있어 트리의 높이를 줄일 수 있음
2. 분기 계수(Branching Factor)의 차이
   • B-트리의 내부 노드는 데이터 공간을 차지하기 때문에 자식 포인터의 개수가 적음
   • B+트리는 내부 노드가 키만 저장하므로 더 많은 자식 노드를 가질 수 있어 트리의 높이를 낮출 수 있음
3. 트리의 균형 유지 특성
   • B-트리의 경우 삽입 및 삭제 작업 시 데이터가 내부 노드에 존재하여 트리의 구조 조정이 더 빈번하게 일어날 수 있음
   • B+트리는 데이터가 리프 노드에만 존재하기 때문에 내부 노드의 구조 조정이 상대적으로 적고, 높이를 낮게 유지할 수 있음

 

B+트리

구조적 특성

• 내부 노드는 키 값만 저장하며, 데이터(디스크 주소)는 저장하지 않고 리프 노드로 가기 위한 포인터만 포함한다.
• 리프 노드에는 모든 키 값과 데이터(디스크 주소)가 저장되며, 리프 노드는 연결 리스트 형태로 서로 연결되어 있어 순차 검색 및 범위 검색이 용이하다.
• 내부 노드와 리프 노드의 키 값의 관계
  1. 내부 노드의 모든 키 값은 리프 노드에 존재하며
  2. 리프 노드의 키 값은 내부 노드에 존재하지 않을 수도 있다..
• 탐색 시 반드시 리프 노드까지 도달해야 한다.*리프 노드 간 연결 리스트를 통해 순차적으로 빠르게 범위 검색이 가능하다. 이는 대규모 데이터베이스 시스템에서 인덱싱 작업에 유리하다.
• 그러나, B-트리 대비 * 탐색 경로가 최적화되어 높이가 낮고 성능이 더 우수하다.

 

B+트리의 내부 노드가 디스크 주소를 저장하지 않는 이유

1. 효율적인 저장 공간 활용
   • 내부 노드가 키 값만 저장하므로, B-트리에 비교해서 동일한 크기의 디스크 블록에 더 많은 키를 저장할 수 있다(디스크 블록 활용 최적화).
   • 이는 트리의 높이를 낮추고 검색 성능을 향상시킨다.
2. 검색 경로 최적화
   • B-트리는 내부 노드에 데이터를 저장하므로, 자식 포인터 개수가 제한된다.
   • B+트리는 내부 노드가 키 값만 저장하므로 더 많은 자식 포인터를 포함할 수 있어 트리의 높이가 더 낮아진다.
   • (하단 이미지) 분기 계수(하나의 노드가 가질 수 있는 최대 자식 노드의 개수) 수식 비교
3. 범위 검색 최적화
   • 범위 검색 시 리프 노드만 순차적으로 탐색하면 되므로 성능이 뛰어나다.
   • 리프 노드가 연결 리스트 형태로 연결되어 있으므로, 연속적인 키 값을 순차적으로 검색할 때 효율적이다.
4. 디스크 I/O 최적화
   • 디스크는 순차 접근이 랜덤 접근보다 빠르기 때문에, 리프 노드 간 연결을 통해 빠르게 데이터를 검색할 수 있다.
   • 탐색 중에는 리프 노드에 도달하기 전까지 디스크 주소를 읽을 필요가 없어 불필요한 I/O를 최소화한다.

분기 계수 수식 비교

 

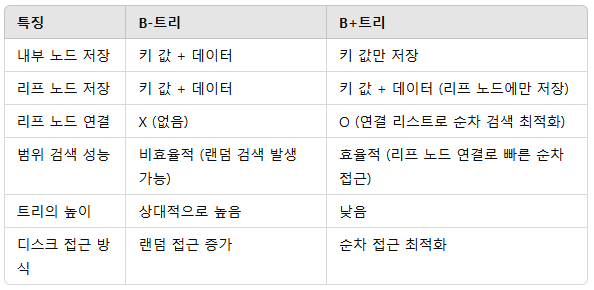
B-트리 vs B+트리 비교